Step-by-step explanation:
we know population growth is an exponential phenomenon. Therefore, the sequence formed will be a geometric sequence. If P_0 is the first term and P_1 is the successive term, then we get:
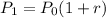
where r is the common ratio or the growth rate. Applying the data of the problem to the previous equation, we get:
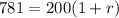
this is equivalent to:
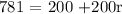
solving for 200r, we get:
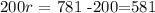
solving for r, we obtain:

Now, if the population grows exponentially, this trend can be modeled using the following formula:
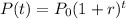
Applying the obtained r value and the data of the problem to the previous equation, we get:
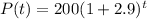
this is equivalent to:
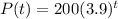
with this formula, we can calculate the number of wolves in 10 years:

Now, if the population grows to 1000 wolves, we get the following equation:
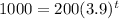
Solving for t, we get:

We can conclude that the correct answer is:
Answer:
a) r = 2.9 ( as a percent would be 290%)
b) 162808121.7
c) 1.2 years