Question

#19 i’m pretty sure i know the awnser but i want to make sure

Answer 1

Increasing: [-1, ∞)

Decreasing: (-∞, -1]

Explanations:

The given graph is a quadratic graph with the parent function expressed as:

`f(x)=x^2`

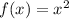
The graph shows a downward shift by 3 units and left shift by 1 unit to give the function:

`g(x)=(x+1)^2-3`

In order to determine the point where the graph is increasing or decreasing, we need to determine the minimum point of the parabola. The minimum point of the parabola is at (-1, -3)

The curve is increasing from the x-coordinate of the minimum point up to infinity (the arrow shows it extends to infinity). Hence the interval of increase is [-1, ∞)

Similarly, the curve is decreasing from infinity down to the x-coordinate of the minimum point (the arrow shows it extends to infinity). Hence the interval of decrease is (-∞, -1].