Given:
Final Balance = $160,000
rate = 8% or 0.08
Compounding period = daily = 365 days
time in years = 10
Find: Principal or Initial Amount
Solution:
To determine the principal or the initial amount to be invested in order to have $160,000 at the end of 10 years with the given compounding rate, we have the formula below:

where:
P = Principal
F = Final Value = $160,000
r = annual rate = 0.08
m = compounding period = 365 days
t = time in years = 10
Let's plug into the formula above the given information.
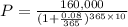
Then, solve for P.
a. Add the terms inside the parenthesis and multiply its exponent.

b. Apply the exponent to the term in the denominator.
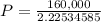
c. Divide the numerator by the denominator.
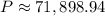
Answer:
Therefore, one must invest $71,898.94 in order to produce a final balance of $160,000 at the end of 10 years given that the rate is 8% compounded daily.