Question

Please help me please I got a picture for you to solve my problem

Answer 1

Area of garden is 4√3 sq. ft.

Given:

A garden is in the shape of an equilateral triangle with sides 4 ft.

The objective is to find the area of the garden.

The formula to find the area of triangle is,

`A=(1)/(2)\cdot b\cdot h`

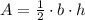
Here, b represents the side of the triangle and h represents the height of the triangle.

The height of an equilateral triangle can be calculated by,

`\begin{gathered} h=(√(3))/(2)\cdot b \\ =\frac{\sqrt[]{3}_{}}{2}\cdot4 \\ =2\sqrt[]{3} \end{gathered}`

Now substitute the value of b and h in the formula of area of triangle.

`\begin{gathered} A=(1)/(2)\cdot4\cdot2\sqrt[]{3} \\ =4\sqrt[]{3}ft^2 \end{gathered}`

Hence, the area of the triangle is 4√3 sq. ft.