Question

Which set of Integers is represents the length of the sides of an a isosceles triangle

Answer 1

Consider that atriangle is said to be an isosceles triangle if its two sides are equal.

Since the set of integers represent the length of sides, two values must be identical for an isosceles triangle.

Therefore, options C and D are ruled out, as all three integers are different in both sets.

Now,consider that any three side measures can form a triangle if the following condition is satisfied,

`\text{Largest Side}<\text{ Sum of the remaining two sides}`

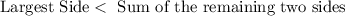
Consider option A,

`\begin{gathered} 6<6+5 \\ 6<11 \end{gathered}`

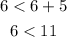
As the statement holds true, the given set of integers (6,6,5) can form a triangle.

Consider option B,

`\begin{gathered} 3<1+1 \\ 3<2 \end{gathered}`

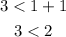
As the statement is false, the given set of integers (1,1,3) cannot form a triangle.

Thus, option A contains the set of values that will form a triangle whose two sides are equal, that is, an isosceles triangle.

Therefore, option A is the correct choice.