Question

А group of college students bought a couch for $80. However, five of them failed to pay their share so the others had to each pay $8 more. How many students were in the original group?

Answer 1

Number of students

А group of college students bought a couch for $80. Let's say that the number of the students in that group is A.

Five of them failed to pay their share so the others had to each pay $8 more. Then the number of students that finally paid it was A - 5.

We have to find the value of A.

We know that in the beggining $80/A was the amount of money each student had to pay.

Then, each one had to pay $80/(A-5).

Since they had to pay $8 more than the initial amount, each one had to pay ($80/A) + $8 .

Then $80/(A-5) = ($80/A) + $8

Now, we have to find A from the previous equation

`\begin{gathered} (80)/(A-5)=(80)/(A)+8 \\ (80)/(A-5)-(80)/(A)=8 \\ (80A-80\mleft(A-5\mright))/((A-5)A)=8 \\ (80A-80A+400)/(A^2-5A)=8 \\ (400)/(A^2-A)=8 \\ (400)/(8(A^2-A))=1 \\ (50)/(A^2-5A)=1 \\ 50=A^2-5A \\ 0=A^2-5A-50 \\ 0=(A-10)(A+5) \end{gathered}`

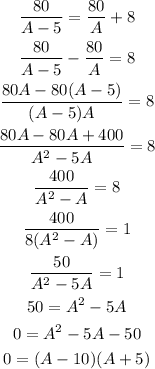
SThen A has two possible values

A₁ = (1 + √201)/2

A₂ = (1 - √201)/2

Since A should be possitive and 1 - √201 is negative then,

A = (1 + √201)/2

≅ (1 + 14) /2 = 15 / 2

= 7.5 ≅ 8

Answer: 8 students were in the original group