Number of students
А group of college students bought a couch for $80. Let's say that the number of the students in that group is A.
Five of them failed to pay their share so the others had to each pay $8 more. Then the number of students that finally paid it was A - 5.
We have to find the value of A.
We know that in the beggining $80/A was the amount of money each student had to pay.
Then, each one had to pay $80/(A-5).
Since they had to pay $8 more than the initial amount, each one had to pay ($80/A) + $8 .
Then $80/(A-5) = ($80/A) + $8
Now, we have to find A from the previous equation
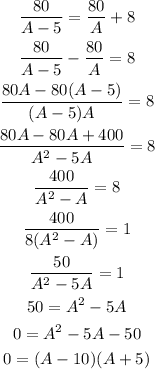
SThen A has two possible values
A₁ = (1 + √201)/2
A₂ = (1 - √201)/2
Since A should be possitive and 1 - √201 is negative then,
A = (1 + √201)/2
≅ (1 + 14) /2 = 15 / 2
= 7.5 ≅ 8
Answer: 8 students were in the original group