Question

If we reduce the number of vertices of a convex polygon P by 20%, the number of its diagonals decreases by 37.5%. How many vertices does P have?

Answer 1

35 vertices

Explanation:

Given a convex polygon with n-vertices, the number of diagonals in the polygon is given by the formula:

`(n(n-3))/(2)`

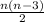
If n is reduced by 20%, the new value of n will be:

`(100-20)\%\text{ of n}=(80)/(100)n=0.8n`

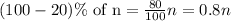
Replace n in the formula above with 0.8n:

Next, we are told that the number of its diagonals decreases by 37.5%. Using the original formula for the number of diagonals, we have:

`\begin{gathered} (1-0.375)*(n(n-3))/(2) \\ =(0.625n(n-3))/(2)\cdots(2) \end{gathered}`

Equate (1) and (2):

`(0.8n(0.8n-3))/(2)=(0.625n(n-3))/(2)`

We solve the equation for n:

`\begin{gathered} 0.8n(0.8n-3)=0.625n(n-3) \\ 0.64n^2-2.4n=0.625n^2-1.875n \\ 0.64n^2-0.625n^2=2.4n-1.875n \\ 0.015n^2=0.525n \\ \text{ Divide both sides by 0.015n} \\ (0.015n^2)/(0.015n)=(0.525n)/(0.015n) \\ n=35 \end{gathered}`

The polygon P has 35 vertices.