Question

Use the Factor Theorem to find all real zeros for the given polynomial function. One of the factor is given. f(x) = 3x^3 + x^2 - 20x + 12; x+3; yes, the binomial is a factor of the polynomial. ; yes, the binomial is a factor of the polynomial. ; the binomial is not a factor of the polynomial. ; the binomial is not a factor of the polynomial.

Answer 1

`f(x)=3x^3+x^2-20x+12`

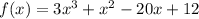
To determine whether (x + 3) is a factor, let's equate it to zero and solve for x.

`\begin{gathered} x+3=0 \\ x+3-3=0-3 \\ x=-3 \end{gathered}`

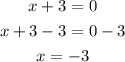
So, let's assume that x = -3. If f(x) = 0 at x = - 3, then (x + 3) is a factor of the polynomial. Let's check.

Replace "x" in the polynomial by -3.

`f(-3)=3(-3)^3+(-3)^2-20(-3)+12`

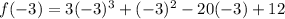
Then, simplify.

`f(-3)=-81+9+60+12`
`f(-3)=0`

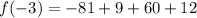
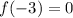
Since f(x) = 0 when x = -3, then yes, (x + 3) is a factor of the polynomial.

Answer:

f(-3) = 0; yes, the binomial (x + 3) is a factor of the polynomial. (Option 2)