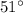Answer:
The measure of arc KD is;
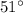
Step-by-step explanation:
Given the figure in the attached image.
Chord LD and MK intercept at N and also intercept the arc of the circle to form arc LM and KD.
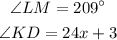
the angle LNM formed by the two chords is given as;
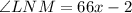
Recall that the angle formed by two intercepting chords can be calculated using the formula;
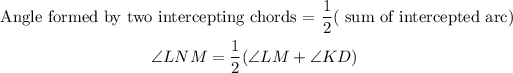
Substituting the given values;
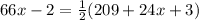
solving for x;
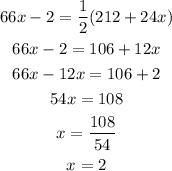
We have the value of x, let us now solve for the measure of arc KD by substituting the value of x;
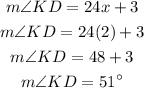
Therefore, the measure of arc KD is;