Question

Solve for X assume that lines which appear tangent are tangent. Find m

Answer 1

The measure of arc KD is;

`51^(\circ)`

Step-by-step explanation:

Given the figure in the attached image.

Chord LD and MK intercept at N and also intercept the arc of the circle to form arc LM and KD.

`\begin{gathered} \angle LM=209^(\circ) \\ \angle KD=24x+3 \end{gathered}`

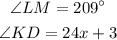
the angle LNM formed by the two chords is given as;

`\angle LNM=66x-2`

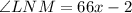
Recall that the angle formed by two intercepting chords can be calculated using the formula;

`\begin{gathered} \text{ Angle formed by two intercepting chords = }(1)/(2)(\text{ sum of intercepted arc)} \\ \angle LNM=(1)/(2)(\angle LM+\angle KD) \end{gathered}`

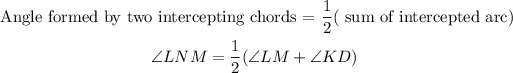
Substituting the given values;

`66x-2=(1)/(2)(209+24x+3)`

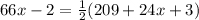
solving for x;

`\begin{gathered} 66x-2=(1)/(2)(212+24x) \\ 66x-2=106+12x \\ 66x-12x=106+2 \\ 54x=108 \\ x=(108)/(54) \\ x=2 \end{gathered}`

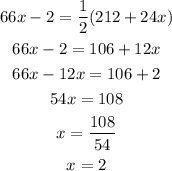
We have the value of x, let us now solve for the measure of arc KD by substituting the value of x;

`\begin{gathered} m\angle KD=24x+3 \\ m\angle KD=24(2)+3 \\ m\angle KD=48+3 \\ m\angle KD=51^(\circ) \end{gathered}`

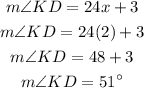
Therefore, the measure of arc KD is;

`51^(\circ)`