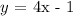We will investigate how to determine the y-intercept of an equation of a line.
A general equation of a line is given in a slope-intercept form as follows:
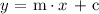
Where,
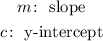
The slope of the line is already determined and expressed as follows:
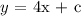
To determine the y-intercept of an equation of a line we need a coordinate pair. We are given a table of values through which the line passes. We can use any of the coordinate pair. We will pick the first pair:
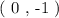
We will plug in the respective coordinate values in the given equation and solve for y-intercept ( c ) as follows:
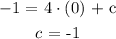
Therefore, the value of the y-intercept when plugged in the general equation we have: