ANSWER:
There is a real zero in this interval
Explanation:
We have the following function:
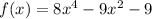
To determine if there is a real zero between 1 and 2, we must evaluate the function at these points, if there is a change from positive to negative or vice versa, by the intermediate value theorem we can say that it has a real zero in that interval.
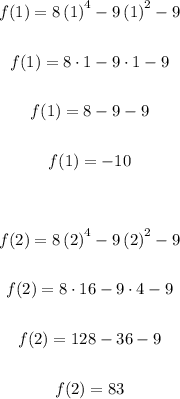
We can observe that it goes from a negative value to a positive value in this small interval, which by means of the theorem we can say that if there is a real zero in this interval