Question

How do I solve this? I know what domain is but how do I solve it like this

Answer 1

`\begin{gathered} a)D=\:\left(-\infty\:,\:0\right)\cup\left(0,\:\infty\:\right) \\ b)D=\:\left(-1,\:\infty\:\right) \end{gathered}`

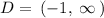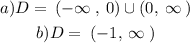
1) The first thing we need to do is to find the composite function. So, based on the ones we've got, we can do the following to get the f(g(x)) functions:

a)

`\begin{gathered} f(x)=2^x,g(x)=(2)/(x) \\ f(g(x))=2^{(2)/(x)} \end{gathered}`

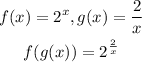
Note that we have plugged into the x term of f(x) the whole function f(x). Now that we know the composite function, we can analyze it.

As the Domain is the set of entries for any function, we need to find the points of singularity, i.e. when the function is not defined.

`\begin{gathered} f(g(x))=2^{(2)/(x)}\:\:\:Pick\:the\:denominator\:and\:equate\:it\:to\:zero \\ \\ x=0 \\ --- \\ Thus, \\ D=\:\left(-\infty\:,\:0\right)\cup\left(0,\:\infty\:\right) \end{gathered}`

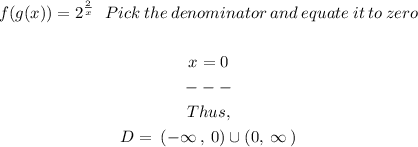
Note that when x=0, then there is an undefinition within the Real Set of Numbers. So, any point different than zero is an element of this Domain.

b)

In this case, we can find the composite function this way:

`\begin{gathered} f(x)=\log(x),\:g(x)=x^3+1 \\ \\ f(g(x))=\log(x^3+1) \end{gathered}`

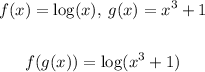
Now, similarly to the previous one let's find the singularity points. We know that x has to be greater than -1 since the argument of a logarithm has to be greater than 0, according to the logarithm definition.

Thus the Domain is:

`D=\:\left(-1,\:\infty\:\right)`