According to the Law of Conservation of Linear Momentum, the total linear momentum of the system formed by the two cars must remain the same before and after the collision.
The linear momentum p of an object with mass m and speed v is:
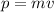
Before the collision, the linear momentum of the car at rest is 0 and the linear momentum of the moving car is:
![p_i=(1000\operatorname{kg})*(13.67(m)/(s))=13,670\operatorname{kg}(m)/(s)]()
After the collision, both cars move together at an unkown speed v. They can be cosnidered a single object whose mass is the sum of the masses of the cars. Then, the linear momentum of both cars combined after the collision, is:
![\begin{gathered} p_f=(1000\operatorname{kg}+1879\operatorname{kg})* v \\ =2879\operatorname{kg}* v \end{gathered}]()
Since the linear momentum before and after the collision is the same, then:
![2879\operatorname{kg}* v=13,670\operatorname{kg}(m)/(s)]()
Solve for v:
![\begin{gathered} \Rightarrow v=\frac{13,670\operatorname{kg}(m)/(s)}{2879\operatorname{kg}}=4.74817645\ldots(m)/(s) \\ \therefore v\approx4.748(m)/(s) \end{gathered}]()
Therefore, the resulting velocity of the two cars right after the collision is 4.748 meters per second.