Answer:
The number of plants in the yard after 3 months = 60
Step-by-step explanation:
The number of blackberry plants that started growing in the yard, p₀ = 30
The blackberry plants will spread by 100% a month
p(1) = 30 + 1(30)
p(1) = 60
The yard can only sustain 60 plants, m = 60
The logistic growth model is given as:
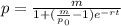
Substitute p₀ = 30, p = 60, t = 1, and m = 60 to solve for the growth rate, r.
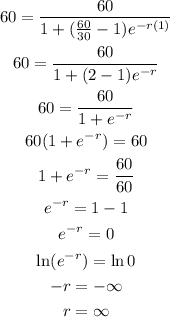
To estimate the number of plants after 3 months:
substitute t = 3, and r = ∞ into the logistic model
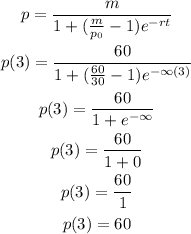
The number of plants in the yard after 3 months = 60