Question

The first half of this problem is complete, but I dont understand how to do the second part.

Answer 1

Okay, here we have this:

According with the provided info we obtain the following equation:

`v=30\cdot((1)/(2))^{(t)/(36)}`

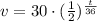
Let's calculate first the 20% of the initial leval:

`30\cdot(20)/(100)=(600)/(100)=6mg`

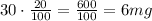
Now, let's replace in the equation "v" with 6 to find the estimated time:

`\begin{gathered} v=30\cdot((1)/(2))^{(t)/(36)} \\ 6=30\cdot((1)/(2))^{(t)/(36)} \end{gathered}`

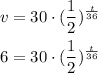
And, finally let's clear t:

`\begin{gathered} 6=30\cdot((1)/(2))^{(t)/(36)} \\ (6)/(30)=((1)/(2))^{(t)/(36)} \\ (1)/(5)=((1)/(2))^{(t)/(36)} \\ (t)/(36)\ln ((1)/(2))=\ln ((1)/(5)) \\ t=(36\ln\left(5\right))/(\ln\left(2\right)) \\ t=83.589 \\ t\approx84 \end{gathered}`

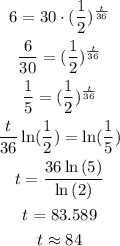
Finally we obtain that after approximately 84 hours the valium concentration will reach 20% of it's initial level.