We have to find the equation of the line that passes through the points (-1,5) and (0,1). We will write the equation in the slope-intercept form, which is given by:

Where m represents the slope of the function, and b the y-intercept. We will find the slope, and then the y-intercept.
1. Finding the slope
For finding the slope we will use the formula:
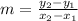
where (x₁,y₁) and (x₂,y₂) are two points that passes through the line. In this case, the points (-1,5) and (0,1).
Replacing, we obtain:
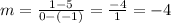
Thus, the slope is -4.
2. Finding the y-intercept
For doing this step, we want to know the value of the function when x equals zero. But, as we have that the line passes through (0,1), this means that this value will be 1. This is, the y-intercept is 1.
3. Putting all together
Now, we just have to put the values obtained in the slope-intercept form:
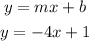
And this means that the equation of the line that passes through (-1,5) and (0,1) is y=-4x+1.