We want to know how many children and adults went to the zoo. In this case, we will call by a to the number of adults, and by c to the number of children.
Since there were 243 people in total, we have that:
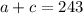
And as the cost for adult is $5 and, $3 for each child, we obtain:

For finding the number of children and adults that went to the zoo, we have to solve tre system:

We will solve it by substitution. On the first equation, we solve for c:
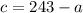
and we replace it onto the second equation:

And we solve for a:
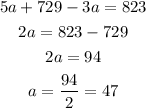
This means that the number of adults is 47. Now, we replace on the first equation, and we get:
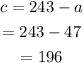
Thus, the number of adults that went to the zoo was 47, and the number of children was 196.