Question

13.4.3 Question Help The Jurassic Zoo charges S5 for each adult admission and $3 for each child. The total bill for the 243 people from a school trip was $823. How many adults and how many children went to the zoo?

Answer 1

We want to know how many children and adults went to the zoo. In this case, we will call by a to the number of adults, and by c to the number of children.

Since there were 243 people in total, we have that:

`a+c=243`

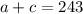
And as the cost for adult is $5 and, $3 for each child, we obtain:

`5a+3c=823`

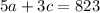
For finding the number of children and adults that went to the zoo, we have to solve tre system:

`\begin{cases}a+c=243 \\ 5a+3c=823\end{cases}`

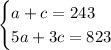
We will solve it by substitution. On the first equation, we solve for c:

`c=243-a`

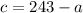
and we replace it onto the second equation:

`5a+3(243-a)=823`

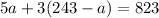
And we solve for a:

`\begin{gathered} 5a+729-3a=823 \\ 2a=823-729 \\ 2a=94 \\ a=(94)/(2)=47 \end{gathered}`

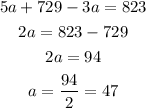
This means that the number of adults is 47. Now, we replace on the first equation, and we get:

`\begin{gathered} c=243-a \\ =243-47 \\ =196 \end{gathered}`

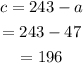
Thus, the number of adults that went to the zoo was 47, and the number of children was 196.