Let A be the first brand and B the second brand, then, we can write

so we have 2 equations in 2 unknows.
Solving by substitution method.
By moving B to the right hand side in the second equation, we have

By substituting this result into equation (a), we have
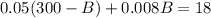
where 18 = 0.06x300. By combining similar terms, we get
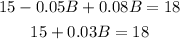
By moving 15 to the right hand side, we obtain
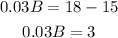
then, B is equal to
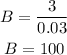
Now, by substituting this result into equation (c), we have
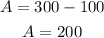
This implies tha the answer is:
First brand: 200 mililiters
Second brand: 100 mililiters