Question

if(x) = x4 - 6x2 +3 Find the intervals where f is concave up and where it is concave down. Locate all inflection points. (You may write on the next page if you need more space for this question.)

Answer 1

You have the following function:

`f(x)=x^4-6x^2+3`

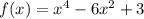
In order to determine the intervals, it is necessary to calculate the first derivative of the function, equal it to zero, and identify the zeros of the equation, just as follow:

`\begin{gathered} f^(\prime)(x)=4x^3-12x=0 \\ 4x(x^2-3)=0 \end{gathered}`

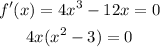
the zeros of the previous equation are:

`\begin{gathered} x_1=0 \\ x_2=\sqrt[]{3} \\ x_3=-\sqrt[]{3} \end{gathered}`

Next, it is necessry if the previous values are minima or maxima. Evaluate the second derivative for the previous values of x. If the result is greater than 0, then, it is a minimum. If the result is lower than zero, it is a maximum:

`\begin{gathered} f^(\prime)^(\prime)(x)=12x^2-12 \\ f^(\prime)^(\prime)(0)=12(0)^2-12=-12<0 \\ f^(\prime)^(\prime)(\sqrt[]{3})=12(\sqrt[]{3})^2-12=24>0 \\ f^(\prime)^(\prime)(-\sqrt[]{3})=12(-\sqrt[]{3})^2-12=24>0 \end{gathered}`

Then, for x=0 there is a maximum, and for x=-√3 and x=√3 there is a minimum.

Hence, until x = -√3 the function decreases. In between x=-√3 and x=0 the function increases. In between x=0 and x=√3 the function decreases and from x=√3 the function increases.

Furthermore, it is necessary to find the inflection points. Equal the second derivative to zero and solve for x:

`\begin{gathered} f^(\prime)^(\prime)(x)=12x^2-12=0 \\ x^2=1 \\ x=\pm1 \end{gathered}`

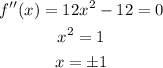
then for x=1 and x=-1 there are inflection points.

The interval where the function is concave up is:

(-∞ , -1) U (1, ∞)

The interval where the function is concave down is:

(-1,1)