To answer this question, we can proceed as follows:
1. We have a normal distribution with a mean, μ = 8 ounces, and a standard deviation, σ = 1.2 ounces.
2. We need to determine the value, x, in the distribution for which the cumulative probability is less than 2.5%.
3. To do this, we can use the z-scores, and they are defined as:
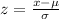
And we already know that:
• μ = 8 ounces
,
• σ = 1.2 ounces
4. If we consult the cumulative standard normal distribution table, we need to find the corresponding value for z for a cumulative probability of 2.5%. Then we have:
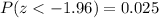
Therefore, we have the corresponding value of z for a cumulative probability of 2.5% (=2.5/100) is z = -1.96.
5. Now, to find the value of x, we can proceed as follows:
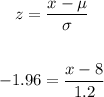
6. Multiply both sides of the equation by 1.2:
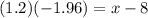
7. And now add 8 to both sides of the equation:
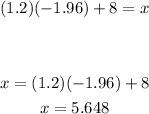
If we round the result to the nearest tenth, we have x = 5.6 ounces.
And we can see that in the following graph:
Therefore, according to the graph, 2.5% of adults eat less than 5.6 ounces of chicken in one sitting (second option).