we are given points A and B that belong to a line and points B and C that belong to another line that is parallel to the first one. We will first find the line that goes through points B and C. First, we will find the slope of this line, using the following formula:
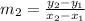
We have the following points:
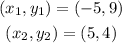
replacing in the equation, we get:
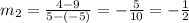
Since the lines are parallel, we have the following relationships between the slopes of each line:
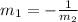
replacing the known values we get:
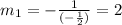
Now we can apply the formula for the slope of these lines, using the following points:
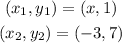
Replacing the known values we get:
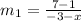
replacing the value for the slope:
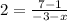
Now we will solve for "x", first by solving the operation in the numerator:
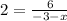
now we will multiply by the expression in the denominator on both sides:
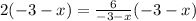
Simplifying:
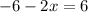
Now we will add 6 on both sides:

Now we will divide by "-2"
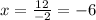
Therefore, the value of "x" for the two lines to be parallel is -6