Consider that the equation of a line with slope 'm' and y-intercept 'c' is given by,
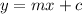
Convert the given equation,
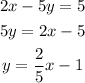
So the slope of the given equation is,
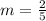
Let the equation of the perpendicular line be,
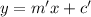
For the lines to be parallel, the product of slopes must be -1.
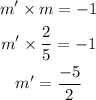
So the equation becomes,
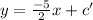
Given that the perpendicular passes through the point (2,-9),
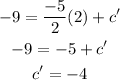
Substitute the value in the equation,
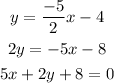
Thus, the equation of the perpendicular line is 5x + 2y + 8 = 0 .