Question

The coordinates for a quadrilateral are W(-8, -3), X(-7, 7), Y(3, 6) and Z(2, -4). Determinethe type of quadrilateral.

Answer 1

square

EXPLANATION :

From the problem, we have the coordinates of the quadrilateral :

`\begin{gathered} W(-8,-3) \\ X(-7,7) \\ Y(3,6) \\ Z(2,-4) \end{gathered}`

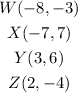
Plot these points to the rectangular coordinate system.

It looks like a square or a rhombus, but we need to make sure of it.

We need to check the distance between two points.

Note that the side lengths of a square and a rhombus are congruent or equal.

Using the distance formula :

`\begin{gathered} d=√((x_2-x_1)^2+(y_2-y_1)^2) \\ d_(WX)=√((-7+8)^2+(7+3)^2)=√(101) \\ d_(XY)=√((3+7)^2+(6-7)^2)=√(101) \\ d_(YZ)=√((2-3)^2+(-4-6)^2)=√(101) \\ d_(ZW)=√((-8-2)^2+(-3+4))=√(101) \end{gathered}`

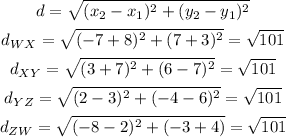
The side lengths are all equal to √101

So it is either square or rhombus

A square has an interior angle of 90 degrees.

For the sides to have a 90 degrees angle, the slope must be negative reciprocal of each other.

The slope formula is :

`\begin{gathered} m=(y_2-y_1)/(x_2-x_1) \\ \\ m_(WX)=(7+3)/(-7+8)=10 \\ \\ m_(XY)=(6-7)/(3+7)=-(1)/(10) \end{gathered}`

Side WX has a slope of 10

and side XY has a slope of -1/10

The slopes are negative reciprocal of each other. Therefore, the quadrilateral is a square