Question

Solve the system using Gaussian elimination or Gauss-Jordan elimination.1)2(x - 2z) = 3y + x + 30x = 2y - 2z - 3-5x + 2y + 6z= -41

Answer 1

Using Gaussian elimination, we have to look for a matrix-like

1 0 0 | a

0 1 0 | b

0 0 1 | c

Where a, b, and c are independent terms.

First, we have to order each equation, variables on the left side and independent terms on the right side.

`\begin{gathered} 2(x-2z)=3y+x+30 \\ 2x-4z=3y+x+30 \\ 2x-4z-3y-x=30 \\ x-3y-4z=30 \end{gathered}`
`\begin{gathered} x=2y-2z-3 \\ x-2y+2z=-3 \end{gathered}`

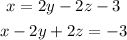
So, the ordered system would be

`\begin{gathered} x-3y-4z=30 \\ x-2y+2z=-3 \\ -5x+2y+6z=-41 \end{gathered}`

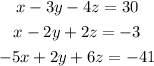
Now, we can form the matrix.

1 -3 -4 | 30

1 -2 2 | -3

-5 2 6 | -41

As we said at the beginning, the Gaussian elimination consists of finding the diagonal of 1 and the zeros. To accomplish that, we operate the rows of the matrix, we can sum and subtract the rows each other, also we can multiply them by a number in order to solve it.

First, we subtract the second row and the first row to get a new second row.

1 -2 2 -3

-1 3 4 -30

0 1 6 -33 (new second row).

Then, the matrix is

1 -3 -4 | 30

0 1 6 | -33

-5 2 6 | -41

Now, we multiply the first row by 5 to subtract it with the third row to get a new third row.

1*5 -3*5 -4*5 | 30*5 = 5 -15 -20 | 150

-5 2 6 | -41

0 -13 -14 | 109 (new third row).

So, the matrix would be

1 -3 -4 | 30

0 1 6 | -33

0 -13 -14 | 109

Then, we multiply the second row by 13 to subtract it with the third row.

0*13 1*13 6*13 | -33*13 = 0 13 78 | -429

0 -13 -14 | 109

0 0 64 | -320 (new third row)

The new matrix is

1 -3 -4 | 30

0 1 6 | -33

0 0 64 | -320

At this point, we can express the matrix as a system of the equation because from here we can find the variables. So, the system that represents the new matrix is-

`\mleft\{\begin{aligned}x-3y-4z=30 \\ 0x+y+6z=-33 \\ 0x+0y+64z=-320\end{aligned}\mright.`

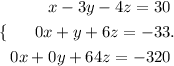
We can solve the third equation to find z.

`\begin{gathered} 64z=-320 \\ z=-(320)/(64) \\ z=-5 \end{gathered}`

Then, we use this value in the second equation to find y.

`\begin{gathered} y+6z=-33 \\ y+6(-5)=-33 \\ y-30=-33 \\ y=-33+30 \\ y=-3 \end{gathered}`

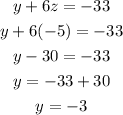
At last, we use the values we found in the first equation to find x.-

`\begin{gathered} x-3y-4z=30 \\ x-3(-3)-4(-5)=30 \\ x+9+20=30 \\ x=30-20-9 \\ x=1 \end{gathered}`

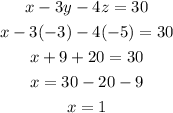
Therefore, the solutions of the system are x = 1, y = -3, and z = -5.