Question

what are the key features of f(x)=8^x? (grapg on deamos domainrange y-intasymptoteth graph is increase or decrease

Answer 1

We have the function y=8^x. This is an exponential function.

The domain is the set of values of x for which the functions is defined. We have no restriction for the values of x because y is defined for all real values of x, so the domain is:

`D=\mleft\lbrace x\mright|\text{ all real numbers}\}`

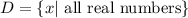
The range is the set of values of y for the domain for which the function is defined.

We know that y will not take negative values: any value of x as input will give us a positive value of y, so the range can be defined as:

`R\colon\mleft\lbrace y\mright|y>0\}`

The y-intercept is the value of y when the function intersects the y-axis. This happens when x=0. Then, the y-intercept is:

`y(0)=8^0=1`

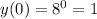
We know that there are no vertical assymptotes, because there is no singularity in the function (the function is defined for all real numbers), so we will look for horizontal assymptotes:

`\begin{gathered} 1)\lim _(x\longrightarrow\infty)8^x=\infty \\ 2)\lim _(x\longrightarrow-\infty)8^x=\lim _(x\longrightarrow)(1)/(8^(-x))=(1)/(\infty)=0 \end{gathered}`

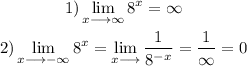
As we have a finite number for the second limit, we have an assymptote at y=0.

We can see if the function is increasing or decreasing by comparing:

`\begin{gathered} a>b \\ f(a)=8^a \\ f(b)=8^b \\ (f(b))/(f(a))=(8^b)/(8^a)=8^(b-a)>1\Rightarrow f(b)>f(a) \end{gathered}`

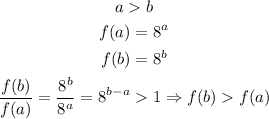
As the function value increases with the increase of x, we know that the function is increasing for all the values of the domain.

We can graph the function as:

Answer:

Domain: D: all real numbers

Range: R: y>0

Y-intercept: y(0) = 1

Assymptote: y=0

The function is increasing for all values of x.