Question

Given the ellipse (x−3)^2/4+(y−4)^2/25=1,Find the center point: List the four vertices

Answer 1

The equation of the ellipse of center (h, k) is

`((x-h)^2)/(b^2)+((y-k)^2)/(a^2)=1`

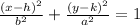
Its 4 vertices are

`(h,k+a)(h,k-a),(h+b,k),(h-b,k)`

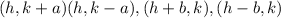
Since the given equation is

`((x-3)^2)/(4)+((y-4)^2)/(25)=1`

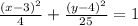
Then by comparing it with the form above

`h=3,k=4`
`b^2=4,b=2,-2`
`a^2=25,a=5,-5`

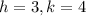
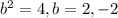
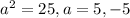
Then we can find the 4 vertices using the rule above

`(h,k+a)=(3,4+5)=(3,9)`
`(h,k-a)=(3,4-5)=(3,-1)`
`\begin{gathered} (h+b,k)=(3+2,4)=(5,4) \\ (h-b,k)=(3-2,4)=(1,4) \end{gathered}`

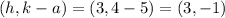
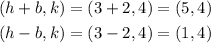
The 4 vertices are

(3, 9), (3, -1), (5, 4), (1, 4)

The center is (3, 4)