Question

2.6.PS-10Challenge Emily and Andy each go to a hardware store to buy wire. Thetable shows the cost y in dollars for x inches of the wire they need. Emilyneeds 25 feet of the wire. Andy needs 15 yards of the wire. How much willeach of them spend for wire?HELPPPP MEEEEE

Answer 1

First, we find the equation that represents the situation

`m=(y_2-y_1)/(x_2-x_1)`

Let's replace the points (110,6.60) and (135,8.10) where,

`\begin{gathered} x_1=110 \\ x_2=135 \\ y_1=6.60 \\ y_2=8.10 \end{gathered}`
`m=(8.10-6.60)/(135-110)=(1.5)/(25)=0.06`

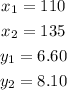
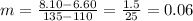
Once we have the slope of the line, we use the point-slope formula to find the equation

`\begin{gathered} y-y_1=m(x-x_1) \\ y-6.60=0.06(x-110) \\ y=0.06x-6.6+6.6 \\ y=0.06x \end{gathered}`

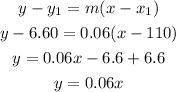
The equation that represents the problem is y = 0.06x.

Now, let's transform 25 feet and 15 yards into inches.

We know that 1 foot is equivalent to 12 inches, so

`25ft\cdot(12in)/(1ft)=300in`

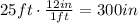
We know that 1 yard is equivalent to 36 inches, so

`15yd\cdot(36in)/(1yd)=540in`

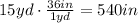
Then, we evaluate the equation for x = 300 and x = 540.

`\begin{gathered} y=0.06x=0.06\cdot300=18 \\ y=0.06x=0.06\cdot540=32.4 \end{gathered}`

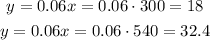
Hence, Emily will spend $18 for 25 feet of wire, and Andy will spend $32.4 for 15 yards of wire.