Question

How does the gravitational field strength at the surface of a planetcompare to the gravitational field strength 1000 m away from thesurface?

Answer 1

Given, the height, h=1000 m

The gravitational field strength of the earth can be obtained by Newton's gravitational law.

The gravitational field strength is also known as acceleration due to gravity.

The gravitational force on an object of mass m due to earth is given by

`\begin{gathered} F=mg=\frac{\text{GMm}}{R} \\ \Rightarrow g=(GM)/(R) \end{gathered}`

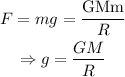
Where g is the acceleration due to gravity, G is the gravitational constant, M is the mass of the earth, and R is the radius of the earth, i.e., the distance between the center of the earth and the object at the surface of the earth.

When the object is at the height h, then the gravitational field strength is given by,

`g_h=(GM)/(R+h)`

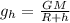
On substituting the known values in the above equation,

`g_h=(GM)/(R+1000)`

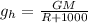
On dividing the equation for the gravitational field strength at the surface of the earth by that at a height h,

`\begin{gathered} (g)/(g_h)=((GM)/(R))/((GM)/(R+1000)) \\ =(R+1000)/(R) \\ =1+(1000)/(R) \end{gathered}`

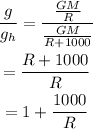
The radius of the earth is R=6.4×10⁶ m

On substituting this,

`\begin{gathered} (g)/(g_h)=1+(1000)/(6.4*10^6) \\ =1+1.56*10^(-4) \\ =1.0002 \\ \approx1 \end{gathered}`

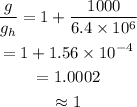
Thus,

`g\approx g_h`

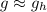
Therefore there is not much difference between the gravitational field strength at a height of 1000 m and that at the surface of the earth.