Question

A 14000 N car traveling at 25 m/s rounds a curve of radius 200 m. What is the magnitude of the net force of the car that is keeping it moving in a circle? ______ N?

Answer 1

Given:

Weight = 14000 N

Velocity = 25 m/s

Radius of curve = 200 m

Let's find the magnitude of the net force of the car that is keeping it moving in a circle.

Let's first find the centripetal acceleration:

`a_c=(v^2)/(r)`

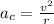
Where:

v = 25 m/s

r = 200 m

We have:

`\begin{gathered} a_c=(25^2)/(200) \\ \\ a_c=(625)/(200) \\ \\ a_c=3.125\text{ m/s}^2 \end{gathered}`

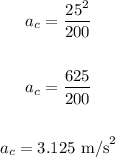
Now, to find the force, apply the formula:

`F=m*a_c`

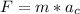
Where:

m is the mass of the car

To find the mass of the car, we have:

`\begin{gathered} m=(F)/(g) \\ \\ Where:g=9.8\text{ m/s}^2 \\ \\ m=(14000)/(9.8)=1428.57\text{ kg} \end{gathered}`

Thus, we have:

`\begin{gathered} F_c=m*a_c \\ \\ F_c=1428.57*3.125 \\ \\ F_c=4464.29\text{ N} \end{gathered}`

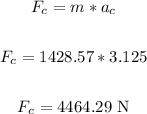
Therefore, the magnitude of the net force that is keeping the car moving in a circle is 4464.29 N.

ANSWER:

4464.29 N