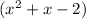Question

Use synthetic division and the given factor to completely factor the polynomial function. x^3+7x^2+4x-12;x+6x^3+7x^2+4x-12=(x+6) = _______. (Factor completely.)

Answer 1

Given:

`x^3+7x^2+4x-12;\text{ x+6}`

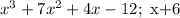
Let's use synthetic division and the given factor to completely factor the polynomial.

To use synthetic division, place the numbers which represents the divisor and the dividend into a long division like method.

To get the divisor, rewrite the expression (x + 6) for x.

Subtract 6 from both sides after equation to zero.

x + 6 = 0

x + 6 - 6 = 0 - 6

x = -6

Hence, the divisor is -6.

Where:

Dividend ==> 1, 7, 4, -12

Divisor ==> -6

We have:

The next step is to bring down the first number (which is 1), multiply the number by the divisor, place the result under the second number, add both numbers, place the result under them.

The, multiply the number by the divisor.

Follow this method until you are done for all numbers.

The quotient will be numbers under the boundary line.

We have the synthetic division below:

Therefore, the quotient is:

`\begin{gathered} 1x^2+1x^-2 \\ \\ =x^2+x-2 \end{gathered}`

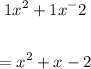
Therefore, the factored form of the polynomial is:

`(x+6)(x^2+x-2)`

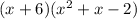
ANSWER:

`(x^2+x-2)`