Question

Can you please help been stuck on this since yesterday I even posted and no one answered

Answer 1

The equation of the parabola is given to be:

`y=x^2+6x-17`

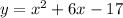
X-INTERCEPTS

To find the x-intercepts, we can substitute y = 0 in the equation. This gives us:

`x^2+6x-17=0`

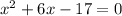
This is a quadratic equation. To solve it, we can use the Quadratic Formula given as:

`x=\frac{-b\pm\sqrt[]{b^2-4ac}}{2a}`

where a and b are the coefficients of the variables with power 2 and 1 respectively and c is the constant term.

We can use the following parameters to solve the question:

`\begin{gathered} a=1 \\ b=6 \\ c=-17 \end{gathered}`

Inputting into the formula, we have:

`\begin{gathered} x=\frac{-6\pm\sqrt[]{6^2-(4*1*\lbrack-17\rbrack)}}{2*1}=\frac{-6\pm\sqrt[]{36+68}}{2} \\ x=\frac{-6\pm\sqrt[]{104}}{2}=(-6\pm10.20)/(2) \end{gathered}`

Therefore, the values for x can be:

`x=(-6+10.20)/(2)=2.10`

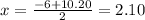
or

`x=(-6-10.20)/(2)=-8.10`

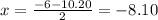
Therefore, the x-intercepts are (-8.10, 0) and (2.10, 0).

Y-INTERCEPT

The y-intercept of the parabola can be gotten by substituting x = 0 into the equation as shown below:

`\begin{gathered} y=(0)^2+6(0)-17 \\ y=-17 \end{gathered}`

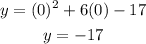
The y-intercept of the parabola is (0, -