Question

Among all the rectangles that have a perimeter of 134 , find the dimensions of the one whose area is largest. write your answers as fractions reduced to the lowest terms.

Answer 1

• Length = 33½ units

,

• Width = 33½ units

Step-by-step explanation:

The perimeter of the rectangle = 134

`\begin{gathered} \text{Perimeter}=2(L+W) \\ 134=2(L+W) \\ L+W=67 \\ \implies L=67-W \end{gathered}`

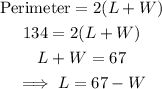
Using the formula for area:

`\begin{gathered} Area=L* W \\ =W(67-W) \\ A=67W-W^2 \end{gathered}`

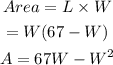
The maximum dimension will occur at the point where the derivative is 0.

`\begin{gathered} A^(\prime)=67-2W=0 \\ 2W=67 \\ W=(67)/(2) \\ W=33(1)/(2)\text{ units} \end{gathered}`

`\begin{gathered} L=67-W \\ =67-33.5 \\ =33(1)/(2)\text{ units} \end{gathered}`

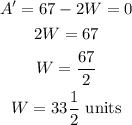
The area is maximum when the width and the length are 33½ units.