Hello there. To solve this question, we'll have to remember some properties about inverse functions.
First, an inverse function is the same as reflecting the function on the function f(x) = x, that is called the identity for inverse functions.
First, graphing the function:
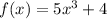
We have
In order to reflect this function, we have to change x by y and solve for y i this case.
Think of this as changing coordinates for which [x y]^T goes to [y x]^T and we want to find the image of this function in this new coordinates.
Changing the variables, we get

Subtract 4 on both sides of the equation
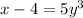
Divide both sides of the equation by a factor of 5
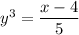
Take the cuberoot on both sides of the equation
![y=\sqrt[3]{(x-4)/(5)}](https://img.qammunity.org/2023/formulas/mathematics/college/b36p4nox75dyf4xgcwbnvg9dq0htwx5iyl.png)
This is the inverse of this function, that we write as
![f^(-1)(x)=\sqrt[3]{(x-4)/(5)}](https://img.qammunity.org/2023/formulas/mathematics/college/z8o350mq9vma2e4tdit96tohp95i6grop4.png)
And its graph is as follows (complementing the first image):