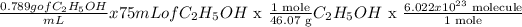Question

How many molecules of C2H-OH would be found in 75.0 ml C2H5OH? The density of C2H5OH is 0.789 g/ml.*Please show the conversion steps

Answer 1

We are given:

Volume of C2H5OH = 75 mL

density of C2H5OH = 0.789 g/mL

We know that 1 mole = 6.022x10^23 molecules

We can first get the number of moles of C2H5OH by calculating the mass from volume and density then convert mass to number of moles.

density = m/V

m = density x V

m = 0.789 g/mL x 75 mL

m = 59.175 g

Now we can find the number of moles. You can get molar mass of ethanol from adding the molar masses of 2C + 6H + O

n = m/M

n = 59.175 g/46,07 g/mol

n = 1.28 mol

Now that we know the number of moles, we can get the number of molecules.

1 mole = 6.022x10^23

1.28 moles = x molecules

`1.28molC_2H_5OH\text{ x }(6.022x10^(23)moleculesofC_2H_5OH)/(1moleofC_2H_5OH)`

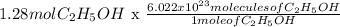
x = 7.735x10^23 molecules.

Therefore 75.0 mL C2H5OH has 7.735x10^23 molecules.

Summary of the calculation:

`(0.789gofC_2H_5OH)/(mL)x75mLofC_2H_5OH\text{ x }\frac{\text{1 mole}}{46.07\text{ g}}C_2H_5OH\text{ x }\frac{6.022x10^(23)\text{ molecule}}{1\text{ mole}}`