Question

In the circuit shown the current is zero. What is the value of V1?(a) 7.59 V(b) 6.38 V(c) 5.62 V(d) 4.41 V

Answer 1

The voltage in a capacitor can be obtained by:

`V_{}=V_s(C_T)/(C_x)_{}`

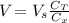
where Cx is tha capacitance of the capacitor, Ct is the equivalent capacitance of the circuit and Vs is the voltage of the circuit.

In this case we have the capacitors in series then the total capacitance is given as:

`(1)/(C_T)=(1)/(C_1)+(1)/(C_2)`

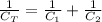
Then in our case we have:

`\begin{gathered} (1)/(C_T)=(1)/(8.25)+(1)/(14.2) \\ (1)/(C_T)=(14.2+8.25)/(117.15) \\ (1)/(C_T)=(22.45)/(117.15) \\ C_T=5.22 \end{gathered}`

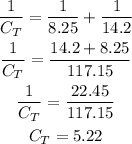
Now that we know that we have for V1:

`\begin{gathered} V=(12)(5.22)/(8.25) \\ V=7.59 \end{gathered}`

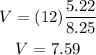
Therefore the value of V1 is 7.59 V and the answer is a.