We know that g(x) = 4x + 3, and that the value of the inverse function of g(x), g^-1(x) has a value of k when its argument is 15.
We can solve it by first calculating the inverse function.
We can start by writing:
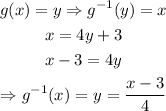
Now, when the argument is x = 15, we get:
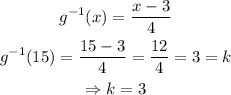
Answer: k = 3