Given:
mean = 85
Standard deviation = 12
Assuming that the data is normally distributed, about 68% of the data would lie one standard deviation from the mean.
Using the z-score formula:
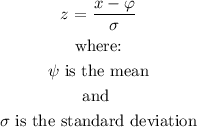
set z= 1:

set z = -1:

Hence, the majority of the data would lie between 73 to 97
Answer:
73 to 97 (Option B)