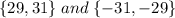Question

The product of two consecutive odd integers is 899. Find the integers.Note: Each set of brackets represents one solution.

Answer 1

The product of two consecutive odd integers is 899.

Let x be the first odd integer.

Then (x+2) will be the second odd integer.

Their product must be equal to 899, so we can write

`x\cdot(x+2)=899`

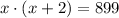
Simplify the equation

`\begin{gathered} x^2+2x=899 \\ x^2+2x-899=0 \end{gathered}`

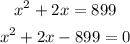
This is a quadratic equation that can be solved by either factoring or using the quadratic formula.

Let's use the quadratic formula.

`x=(-b\pm√(b^2-4ac))/(2a)`

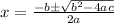
For the given case, the coefficients are

a = 1

b = 2

c = -899

`\begin{gathered} x=\frac{-2\pm\sqrt[]{2^2-4(1)(-899)}}{2(1)} \\ x=\frac{-2\pm\sqrt[]{3600}}{2} \\ x=(-2\pm60)/(2) \\ x=(-2+60)/(2),\; x=(-2-60)/(2) \\ x=(58)/(2),\; x=(-62)/(2) \\ x=29,\; x=-31 \end{gathered}`

So, the first integer is 29

The second odd integer is x + 2 = 29 + 2 = 31

Verify the results

`29*31=899`

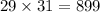
Also, -31 is the first integer.

The second integer is x + 2 = -31 + 2 = -29

Verify the results

`-31*-29=899`

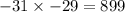
Therefore, the solution is

`\mleft\lbrace29,31\mright\rbrace\; and\; \mleft\lbrace-31,-29\mright\rbrace`