Question

Identify the mean, median, and mode for the dot plot below.Dotplot of Random Values⠀0 1 2 3 4 5 6 7 8 9Random ValuesMean =Median =Mode =andType the lower number then the higher number

Answer 1

mean = 4.84

median = 4.5

mode = 7 and 9

EXPLANATION :

From the problem, we have a dot plot. The dots represent the frequency of each item.

0 has a frequency of 3

1 has a frequency of 3

2 has a frequency of 7

3 has a frequency of 6

4 has a frequency of 6

5 has a frequency of 3

6 has a frequency of 4

7 has a frequency of 8

8 has a frequency of 2

and 9 has a frequency of 8

The total items or data is the sum of frequencies.

That will be :

`3+3+7+6+6+3+4+8+2+8=50`

Recall that the mean is the average of the data.

To get this, get the sum of the products between the data and their frequencies divided by the total data.

That will be :

`(0(3)+1(3)+2(7)+3(6)+4(6)+5(3)+6(4)+7(8)+8(2)+9(8))/(50)=4.84`

The mean is 4.84

Median is the middle term when the data is arranged from least to greatest.

Since there are 50 items, the middle term is between 25th and 26th term.

Let's rewrite the data from lowest to greatest.

0, 0, 0, 1, 1, 1, 2, 2, 2, 2, 2, 2, 2, 3, 3, 3, 3, 3, 3, 4, 4, 4, 4, 4, "4", "5", 5, 5, 6, 6, 6, 6, 7, 7, 7, 7, 7, 7, 7, 7, 8, 8, 9, 9, 9, 9, 9, 9, 9, 9

The 25th term is 4 and the 26th term is 5.

Since the median is between these two terms, we need to get the average, that will be :

`(4+5)/(2)=4.5`

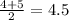
So the median is 4.5

Mode is the data with the most or highest frequency.

In this case, 7 and 9 have both 8 frequencies.

So the modes are 7 and 9