Question

Find the exact value of each of the remaining trigonometric functions

Answer 1

We have an angle theta and we have to calculate the six trigonometric functions.

We know that:

`\begin{gathered} \sin \theta=(2)/(3) \\ \tan \theta<0 \end{gathered}`

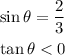
As the sine is positive and the tangent is negative, we can conclude that the cosine is negative.

We can find the cosine of theta using the following identity:

`\begin{gathered} \sin ^2\theta+\cos ^2\theta=1 \\ \cos ^2\theta=1-\sin ^2\theta \\ \cos ^2\theta=1-((2)/(3))^2 \\ \cos ^2\theta=1-(4)/(9) \\ \cos ^2\theta=(9-4)/(9) \\ \cos ^2\theta=(5)/(9) \\ \cos \theta=-\frac{\sqrt[]{5}}{3} \end{gathered}`

Now that we know the sine and the cosine, we can derive all the other trigonometric functiosn as:

`\tan \theta=(\sin\theta)/(\cos\theta)=\frac{(2)/(3)}{-\frac{\sqrt[]{5}}{3}}=-\frac{2}{\sqrt[]{5}}=-\frac{2\sqrt[]{5}}{5}`
`\cot \theta=(1)/(\tan\theta)=-\frac{\sqrt[]{5}}{2}`
`\csc \theta=(1)/(\sin \theta)=(3)/(2)`
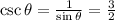
`\sec \theta=(1)/(\cos\theta)=-\frac{3}{\sqrt[]{5}}=-\frac{3\sqrt[]{5}}{5}`

Answer:

cos θ = -√5/3

tan θ = -2√5/5

cot θ = -√5/2

csc θ = 3/2

sec θ = -3√5/5