Question

A system of equations is show. Y=-1/2xX^2+y^2=20Which of the following ordered pairs are solutions of the system of equations?Select two correct ordered pairs. A. (8,-4)B. (-4,2)C. (0,0)D. (4,-2)E. (8,-4)

Answer 1

Step-by-step explanation:

For the system of equations given below

`\begin{gathered} y=-(1)/(2)x \\ x^2+y^2=20 \end{gathered}`

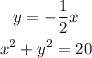
If we are to solve, we will simply substitute y=-1/2x into the second equation, so that

`\begin{gathered} x^2+(-(1)/(2)x)^2=20 \\ x^2+(1)/(4)x^2=20 \\ (4x^2+1x^2)/(4)=(5)/(4)x^2=20 \\ \text{cross multiply} \end{gathered}`
`\begin{gathered} x^2=(20*4)/(5) \\ x^2=16 \\ x=-4 \\ \text{and} \\ x=4 \end{gathered}`

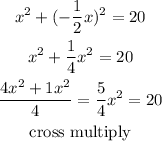
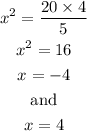
The next step will be to substitute x=4 and x=-4 into the equation to get the required values of y

When x=4

`\begin{gathered} y=-(1)/(2)x \\ y=-(1)/(2)(4)=-2 \\ \text{Thus one of the pair is} \\ (4,-2) \end{gathered}`

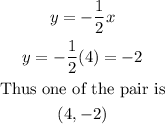
Also,

When x=-4

`\begin{gathered} y=-(1)/(2)x \\ y=-(1)/(2)(-4) \\ y=2 \\ \text{Thus, the second pair is} \\ (-4,2) \end{gathered}`

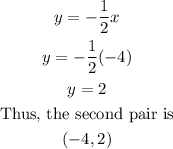
Hence, the answers are: Options B and D