Question

In 1990, approximately 1,820,000 violent crimes were reported in the U.S. By 2019, this number had fallen to approximately 1,200,000.(a) Write a linear model to describe the number of violent crimes in the U.S. from 1990 onward.Pt =(b) Using this linear model, predict the number of violent crimes in 2032. Round your answer to the nearest whole number.violent crimes(c) When do you expect the number of violent crimes to reach 800,000? Give your answer as a calendar year (ex: 2020).During the year

Answer 1

Data:

• A,( 0, 1,820,000)

,

• B,( 29, 1,200,000)

,

• Year 2 - year 1 = 2019 - 1990 = 29

a)

Based on the point A and B, the linear model is as follows:

• Slope ( ,m ,)

`m=\frac{1,200,000-1,820,000}{29\text{ -}0}=-(620,000)/(29)`

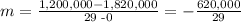
• Parameter b

`\begin{gathered} P(t)=mt+b \\ 1,200,000=-(620,000)/(29)\cdot29+b \\ 1,200,000=-620,000+b \\ b=1,200,000+620,000=1,820,000 \end{gathered}`

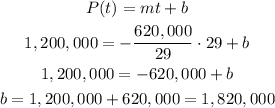
Answer a) (linear model):

`P(t)=-(620,000)/(29)t+1,820,000`

b)

2032-1990 = 42

`\begin{gathered} P(42)=-(620,000)/(29)\cdot42+1,820,000 \\ P(42)=922068.97 \end{gathered}`

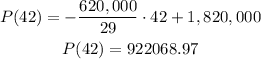
Answer of the number of violent crimes in 2032:

`P(42)=922068.97`

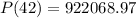
c)

`\begin{gathered} 800,000=-(620,000)/(29)\cdot t+1,820,000 \\ 800,000-1,820,000=-(620,000)/(29)\cdot t \\ -1,020,000=-(620,000)/(29)\cdot t \\ t=(-1,020,000)/(-(620,000)/(29))=47.71 \\ 1990+47.71=2037.71 \end{gathered}`

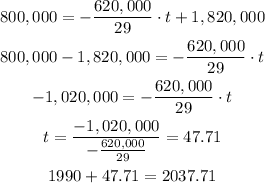
Answer of c: 2037