Question

for the exponential function identify the initial amount the percent change and the growth factor then state whether the function models exponential growth or exponential decay

Answer 1

The function, f(x), given has the form:

`f(x)=a(1+r)^x^{}`

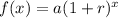
where

• a: initial amount

,

• r: growth or decay rate, as a decimal

In this case, the values of the constants are:

`\begin{gathered} a=20 \\ r=-(3)/(10) \end{gathered}`

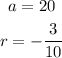
Then, the initial amount is a = 20

To transform the rate into a percent rate of change, we have to multiply it by 100, as follows:

`r=-(3)/(10)=-(3)/(10)\cdot100=-30\%`

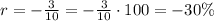
The percent rate of change is -30%

Exponential functions can be also expressed as follows:

`f(x)=ab^x`

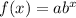
where b is the growth factor. Comparing these functions, we notice that:

`1+r=b`

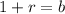
In this case:

`\begin{gathered} b=1-(3)/(10) \\ b=(10-3)/(10) \\ b=(7)/(10) \end{gathered}`

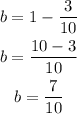
The growth factor is b = 7/10

Given that the growth factor is less than 1, then the function models an exponential decay