Question

Lyra is designing a model of a solar system with a planet and a comet. The planet has a circular orbit, centered at the origin with a diameter of 120. The comet follows a parabolic path with directrix x = 85 and vertex at (75, 0).Part A: Write the equation of the planet's orbit in standard form. Show your work. (2 points)Part B: Write the equation of the comet's path in standard form. Show your work. (4 points)

Answer 1

Given:-

The planet has a circular orbit, centered at the origin with a diameter of 120. The comet follows a parabolic path with directrix x = 85 and vertex at (75, 0).

To find:-

Write the equation of the planet's orbit in standard form and also Write the equation of the comet's path in standard form.

The co-ordinates of center of circle is (0,0) since the diameter is 120 then the radius is 60. so we have,

So the standard equatio is,

`\begin{gathered} x^2+y^2=60^2 \\ x^2+y^2=3600 \end{gathered}`

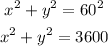
Now we find the equation of comets path in standard form. The diretrix is x = 85 and vertex is at ( 75,0 ).

Now we find the value of a,

`\begin{gathered} (a)/(2)=85-75 \\ (a)/(2)=10 \\ a=20 \end{gathered}`

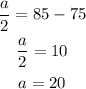
So the equation is,

`(y-y_1)^2=-4a(x-x_1)`

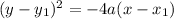
Substituing the required value ( 75,0). we get,

`\begin{gathered} (y-0)^2=-4*20(x-75) \\ y^2=-80(x-75) \end{gathered}`

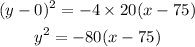
These are the required equations.