Question

Draw a box-and-whisker plot for each data set.5)Annual Precipitation (Inches)41.6 14.848 7023.6 35.644.81712251415.25119.81217.2A)10203040 50 6070B)10:203040 50 60 70C)10 20 30 40 50 60 70 80D)10 20 30 40 5060 70

Answer 1

We are asked to draw a box-and-whisker plot for the given data of annual precipitation.

Recall that a box-and-whisker plot shows five statistical measures.

1. Minimum value

2. Lower quartile

3. Median

4. Upper quartile

5. Maximum value

Let us calculate these five measures from the given data set.

First of all, arrange the data in ascending order (least to greatest)

5.8, 7.2, 7.2, 14.8, 15.2, 17.2, 17.2, 19.8, 23.6, 35.6, 41.6, 44.8, 48, 51, 51.4, 70

As you can see from the above data,

Minimum value = 5.8

Maximum value = 70

The median of the data set is given by

Where n is the number of data points (that is 16)

So, the median is 21.7

Now let us find the lower and upper quartiles

`lower\: quartile=(1)/(4)(n)=(1)/(4)(16)=4th`

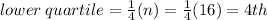
The value at the 4th position is 14.8

Lower quartile = 14.8

`upper\: quartile=(3)/(4)(n)=(3)/(4)(16)=12th`

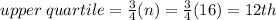
The value at the 12th position is 44.8

Upper quartile = 44.8

Therefore, the five statistical measures are

1. Minimum value = 5.8

2. Lower quartile = 14.8

3. Median = 21.7

4. Upper quartile = 44.8

5. Maximum value = 70

From the given options, we see that option D exactly matches with the above statistical measures.

Therefore, the correct answer is option D