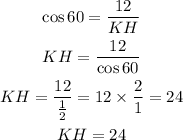Question

Given: JL = 12K кJ1260°45°HJH =HL =JK=KH =:: 12::12V2::12V/3:: 24

Answer 1

Step-by-step explanation:

From the given image of the triangle, let's go ahead and find HL by taking the sine of angle 45 degrees as shown below;

`\begin{gathered} \sin 45=(12)/(HL) \\ HL=(12)/(\sin 45)=\frac{12}{\frac{1}{\sqrt[]{2}}}=12*\sqrt[]{2} \\ HL=12\sqrt[]{2} \end{gathered}`

Let's find JH by taking the tangent of angle 45 degrees;

`\begin{gathered} \tan 45=(12)/(JH) \\ JH=(12)/(\tan 45)=(12)/(1)=12 \end{gathered}`

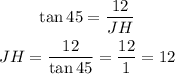
Let's find JK by taking the tangent of angle 60 degrees;

`\begin{gathered} \tan 60=(JK)/(12) \\ JK=12\tan 60 \\ JK=12\sqrt[]{3} \end{gathered}`

Let's find KH by taking the cosine of angle 60 degrees;

`\begin{gathered} \cos 60=(12)/(KH) \\ KH=(12)/(\cos 60) \\ KH=(12)/((1)/(2))=12*(2)/(1)=24 \\ KH=24 \end{gathered}`