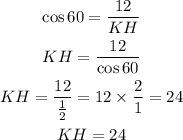Answer:
![undefined]()
Step-by-step explanation:
From the given image of the triangle, let's go ahead and find HL by taking the sine of angle 45 degrees as shown below;
![\begin{gathered} \sin 45=(12)/(HL) \\ HL=(12)/(\sin 45)=\frac{12}{\frac{1}{\sqrt[]{2}}}=12*\sqrt[]{2} \\ HL=12\sqrt[]{2} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/xahlhest0x9j3cqd26674ib2ptiiz9dgz5.png)
Let's find JH by taking the tangent of angle 45 degrees;
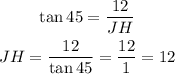
Let's find JK by taking the tangent of angle 60 degrees;
![\begin{gathered} \tan 60=(JK)/(12) \\ JK=12\tan 60 \\ JK=12\sqrt[]{3} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/ia3aavhaiyfs1n7w2b58isbx5bfne5d3vb.png)
Let's find KH by taking the cosine of angle 60 degrees;